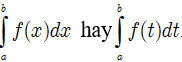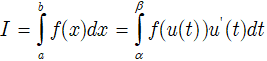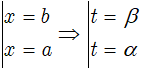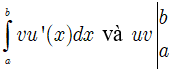1. Định nghĩa, công thức tích phân
* Định nghĩa: Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số F(b) - F(a) được gọi là tích phân của f từ a đến b và kí hiệu:
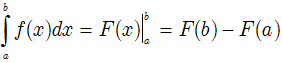
* Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi
Tích phân đó chỉ phụ thuộc vào f và các cận a; b mà không phụ thuộc vào cách ghi biến số.
* Định lí: Cho hàm số y = f(x) liên tục; không âm trên đoạn [a;b]. Khi đó, diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b là:
2. Tính chất của tích phân
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :

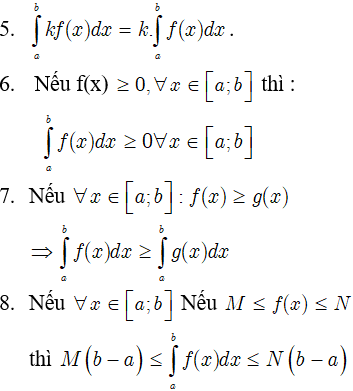
3. Một số phương pháp tính tích phân
3.1. Phương pháp đổi biến số
a) Phương pháp đổi biến số dạng 1
Định lí
1) Hàm x = u(t) có đạo hàm liên tục trên [α;β].
2) Hàm hợp f [u(t)] được xác định trên [α;β].
3) u(α) = a; u(β) = b.
Khi đó:
• Bước 1: Đặt x = u(t).
• Bước 2: Tính vi phân hai vế: x = u(t) ⇒ dx = u'(t)dt. Đổi cận:
• Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t.
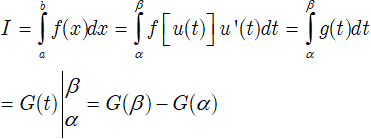
b) Phương pháp đổi biến dạng 2
Định lí: Nếu hàm số u = u(x) đơn điệu và có đạo hàm liên tục trên đoạn [a;b] sao cho f(x)dx = g(u(x))u'(x)dx = g(u)du thì:

Phương pháp chung
• Bước 1: Đặt u = u(x) ⇒ du = u’(x)dx
• Bước 2: Đổi cận:
• Bước 3: Chuyển tích phân đã cho sang tích phân theo u.
Vậy:
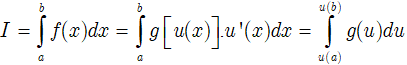
3.2. Phương pháp tích phân từng phần
a. Định lí
Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên [a;b] thì:
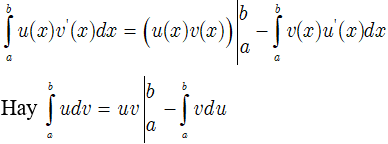
b. Phương pháp chung
• Bước 1: Viết f(x)dx dưới dạng udv = u.v’dx bằng cách chọn một phần thích hợp của f(x) làm u(x) và phần còn lại dv = v'(x)dx
• Bước 2: Tính du = u'dx và v = ∫dv = ∫v'(x)dx
• Bước 3: Tính
* Cách đặt u và dv trong phương pháp tích phân từng phần.
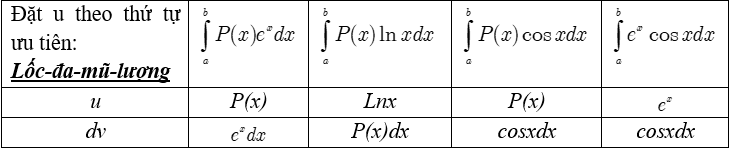
4. Tích phân các hàm số sơ cấp cơ bản
- Tích phân hàm hữu tỉ
- Tích phân hàm vô tỉ
- Tích phân hàm lượng giác
II. BÀI TẬP
Bài số 1. Mức 1 ,2 (30 câu)
Bài số 2. Mức 1 (40 câu)
Bài số 3. Mức 1 (15 câu)